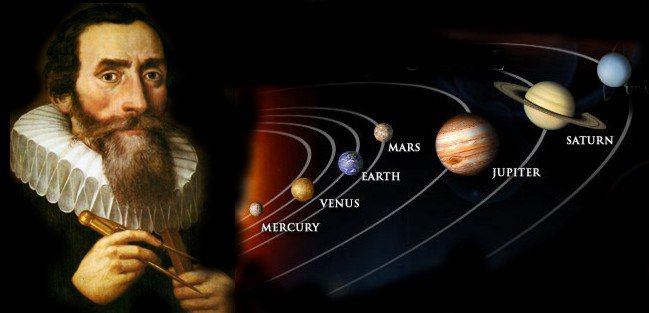
A decisive step was taken in the seventeenth century by Johannus Kepler in Germany, a renowned mathematician, the founding father of modern astronomy.
Protestant of confession and thus little concerned by the recommendations of Rome which was in a blind alley, Kepler did not seek to “save the phenomena” while maintaining at any cost the circle and the geocentric theory to ensure the harmony of the world.
His laws described the movement of planets around the Sun, specifying in particular that the planetary orbits were ellipses [10] whose Sun occupied one of the foci. From 1609, the ellipse replaced the circle in astronomy.
By systematically studying the planet Mars, Kepler empirically gave the laws that bear his name and that allow us in the twenty-first century to explore the solar system or to reach the moon.

If the circle is the only closed orbit with the ellipse, why are the planets and satellites orbiting in elliptical and not circular orbits? In 1609, German astronomer Johannus Kepler mathematically demonstrated that the planets orbited the Sun on ellipses. Why not a circle? The trajectory of planets and satellites would be a circle if they moved in a strictly orthogonal way with respect to the planet-sun or planet-satellite axis without undergoing any disturbance. But all the celestial bodies are practically in mutual interactions with each other more or less pronounced, deflecting them from their trajectory. The trajectories of planets and satellites are conics characterized by the fact that the force of attraction is inversely proportional to the square of the distance. The ellipsis is therefore referred to as an abuse of language, in fact a rough approximation because, strictly speaking, no planetary trajectory is really elliptical because it undergoes permanent orbital perturbations. On the right, the helical model of the solar system (see video above). Below, the orbits of the main bodies of the solar system seen from three different angles. Each image covers about 50 AU. Document Dario Izza/ESA.
whats up!
whats up man!
Heyo
SQ
H